Total pressure is defined as the force exerted by a static fluid on a surface either plane or curved when the fluid comes in contact with the surfaces.
Centre of pressure is defined as the point of application of the total pressure on the surface.
There are generally four cases of submerged surface on which the total pressure force and the centre of pressure is to be determined:
Horizontal plane surface
Vertical plane surface
Inclined plane surface
Curved surface
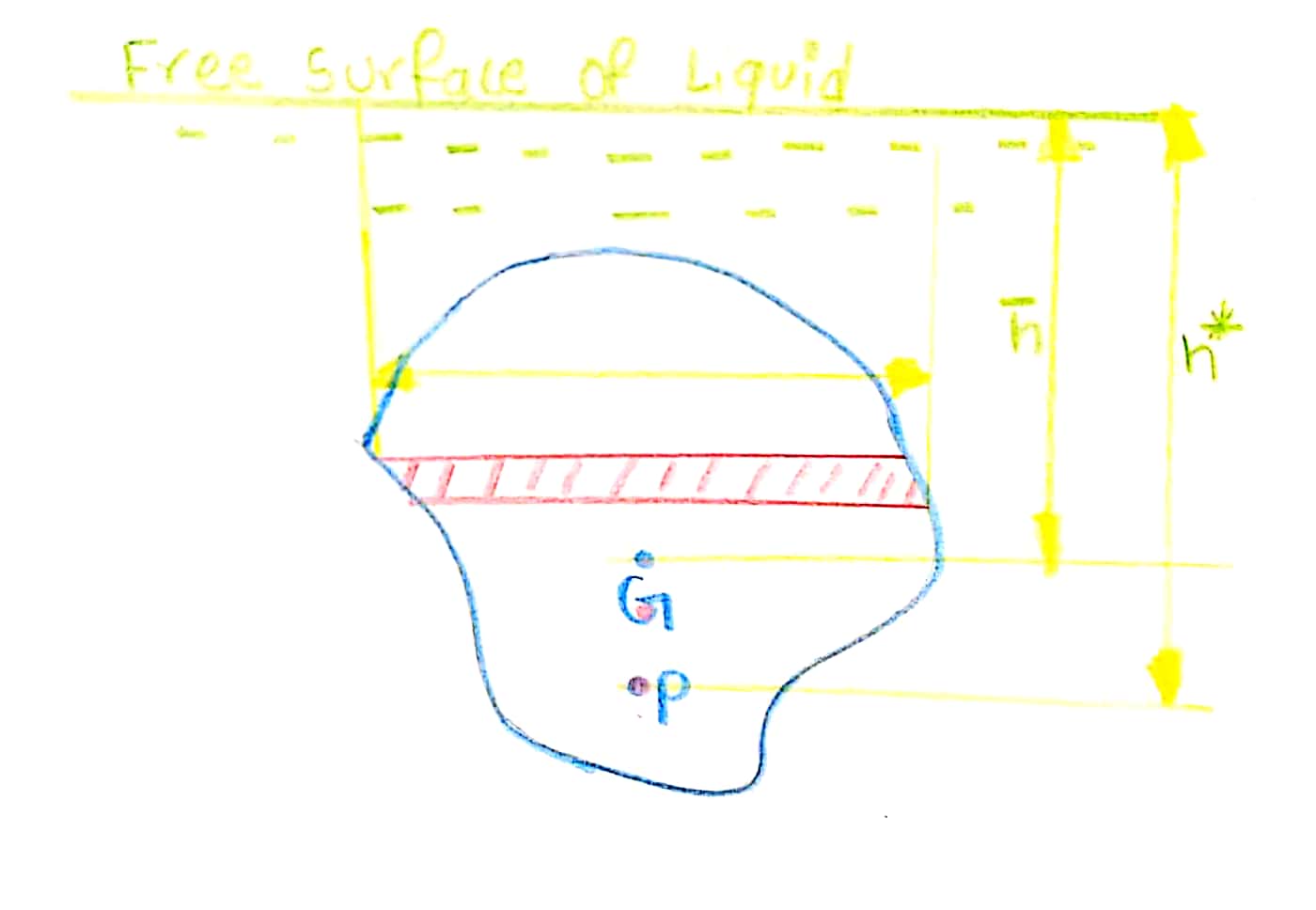
Vertical plane surface submerged in a liquid
Let us consider a plane vertical surface of arbitrary shape as shown in the figure.
Let,
A be the total area of the surface
`bar (h)` be the distance of C.G. of the area from the free surface of the liquid
G be the centre of gravity of the plane surface
P be the centre of pressure
`h^**` be the centre of pressure from free surface of the liquid
Let us consider a strip of thickness dh and width b at a depth h from the free surface of the liquid as shown in figure. Thus area of strip,`dA=b*dh`
Now, the pressure intensity on the strip is,`=rhogh`
The pressure force on the strip is,`dF=P*dA`
`=rhogh*bdh`
The total pressure force on the whole surface is,
`F=\int (rhogh*bdh)=rhog\int (bh*dh)`
But,`\int bh*dh=\inth*dA`
=moment of surface area about the free surface of liquid
=Area of surface ** distance of c.g. from free surface
`=A**bar (h)`
Thus,
`F=rhogA bar (h)`
Now the centre of pressure is calculated by using the principle of moments which states that the moment of the resulting force about an axis is equal to the sum of the moments of the components about the same axis.
The resulting force F is acting at P, at a distance `h^**` from the free surface of liquid as shown in figure. Hence moment of force F about free surface of liquid is `=F*h^**`
Similarly the moment of force dF acting on the strip about free surface of liquid is,
`=dF**h`
`=rhogh**bdh**h`
Sum of moments of all such forces about the free surface of liquid is,
`=\int (rhogh**bdh**h)`
`=rhog \int (h^2*bdh)`
`=rhog \int (h^2 dA)`
But,`\int h^2 dA=\int bh^2 dh=I_0`
=moment of inertia of the surface about the free surface of liquid.
Thus the sum of moments about free surface is,
`rhog*I_0`
or,`F*h^**=rhog*I_0`
`rhogA bar (h)*h^**=rhog*I_0`
`h^**=I_0/(A bar (h))`
Now,From the theorem of parallel axis,
`I_0=I_G+A(bar (h))^2`
Where, `I_G` is the moment of inertia about an axis passing through c.g. and parallel to the free surface of liquid.
Thus,
`h^**=(I_G+A(bar (h))^2)/(Abar (h))`
`h^**=I_G/(A bar (h))+bar (h)`
This is the expression for the centre of pressure which shows that
Inclined plane surface submerged in liquid:
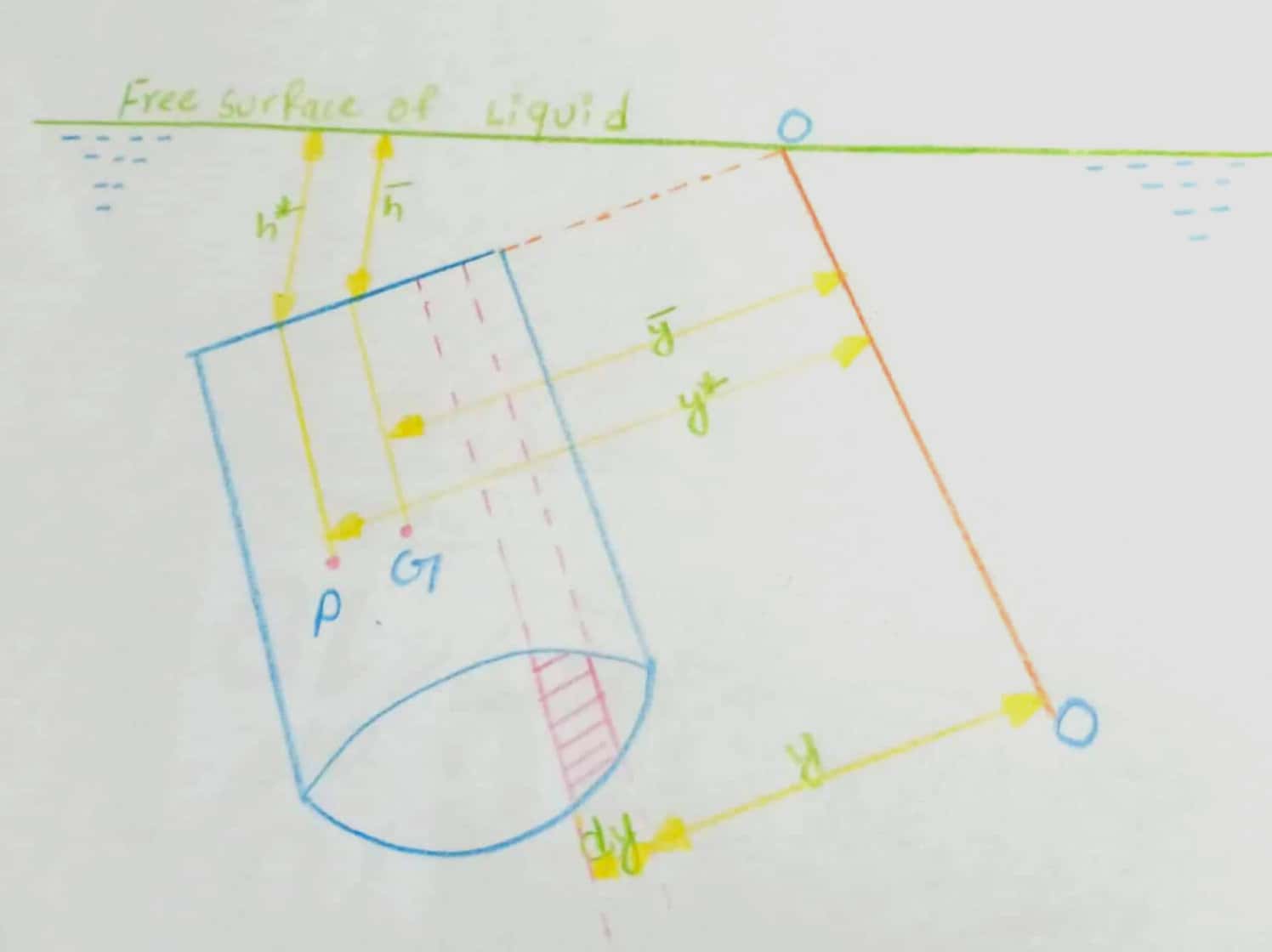
Let us consider a plane surface of arbitrary shape immersed in a liquid in such a way that the plane makes an angle `theta` with the free surface of liquids as shown in figure.
Let,
A be the total area of the inclined surface
`bar (h)` be the distance of C.G. of the area from the free surface of the liquid
G be the centre of gravity of the plane surface
P be the centre of pressure
`h^**` be the centre of pressure from free surface of the liquid
Let the plane of the surface if produced meet the free liquid surface at O. Then O-O is the axis perpendicular to the pane of the paper.
Let,
`bar (y)` be the distance of the c.g. of the inclined surface from O-O
`y^**` be the centre of pressure from O-O.
Let us consider a strip of area dA.at a depth h from the free surface of the liquid and at a distance y from the axis O-O as shown in figure.
Now, the pressure intensity on the strip is,`=rhogh`
The pressure force on the strip is,`dF=P*dA`
`=rhogh*dA`
The total pressure force on the whole surface is,
`F=\int (rhogh*dA)`
From figure,
`h/y=bar (h)/(bar (y))=(h^**)/(y^**)=sintheta`
Thus,`h=ysintheta`
And,
`F=\int (rho*g*ysintheta*dA`
`=rhogsintheta \int(ydA)`
But,
`\int ydA=A*bar (y)`
`F=rhog sintheta*bar (y)*A`
`F=rhogA bar (h)`
Now the centre of pressure is calculated by using the principle of moments which states that the moment of the resulting force about an axis is equal to the sum of the moments of the components about the same axis.
The resulting force F is acting at P, at a distance `y^**` from the O-O axis as shown in figure. Hence moment of force F about free surface of liquid is `=F*y^**`
Similarly the moment of force dF acting on the strip about free surface of liquid is,
`=dF**h`
`=rhog*ysintheta**dA**h`
`=rhog sintheta*y^2 dA`
Sum of moments of all such forces about the O-O is,
`=\int (rhog sintheta*y^2 dA)`
`=rhog *sintheta \int (y^2*dA)`
But,
`\int y^2 dA=I_0`
=moment of inertia of the surface about the O-O.
Thus the sum of moments about O-O is,
`rhog*sintehta*I_0`
Thus,
or,`F*y^**=rhog*sintheta*I_0`
`rhogA bar (h)*h^**=rhog*I_0`
`y^**=(h^**)/(h sintheta)`
Now,From the theorem of parallel axis,
`I_0=I_G+A(bar (h))^2`
Where, `I_G` is the moment of inertia about an axis passing through c.g. and parallel to O-O.
Thus,
`(h^**)/(sintheta)=(rhog sintheta)/(rhogAbar (h))*(I_G+A*(bar (h))^2)`
But,
`bar (h)/bar (y)=sintheta`
`bar (y)=bar (h)/(sintheta)`
`h^**= (sin^2 theta)/(A bar (h))*(I_G+(A (bar (h))^2/(sin^2theta))`
`h^**=(I_G*sin^2 theta)/(A*bar (h))+bar (h)`
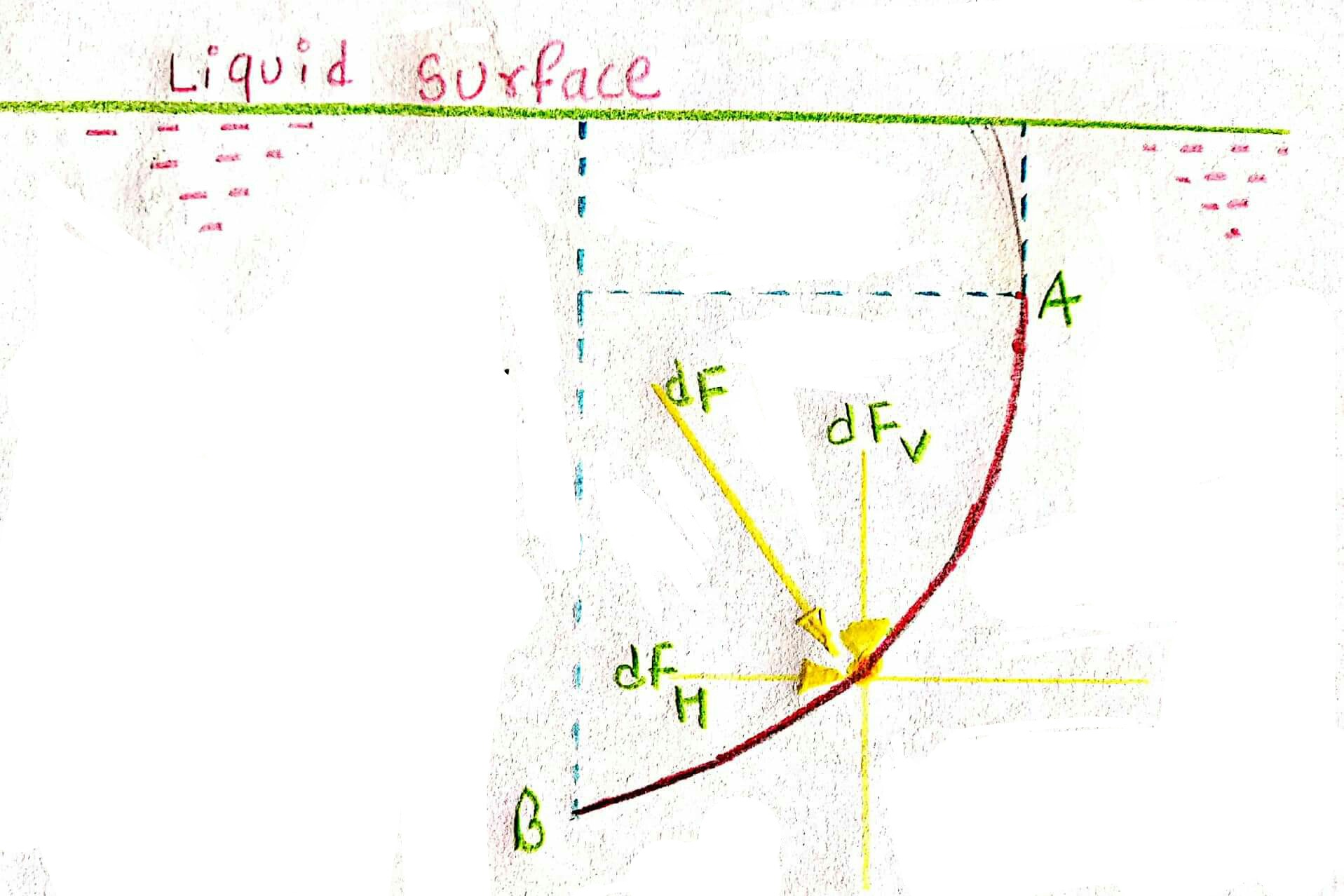
Curved submerged surface
Consider a curved surface AB submerged in a static fluid as shown in figure. Let dA be the area of a small strip at a depth h from water surface.
Then pressure force on the area dA is,
`dF=rhogh*dA`
This force acts normal to the surface.
Hence total pressure force on curved surface should be,
`F=\int rhogh*dA`
But, in case of curved surface the direction of the total pressures on the elementary areas are not in the same direction, but varies from point to point. Thus the integration of above equation for curved surface is impossible.
The problem, however, can be solved by resolving the force F into horizontal and vertical components `F_H` and `F_V`.
Then total force on the curved surface is,
`F=root ()((F_x)^2+(F_y)^2)`
The direction of the resultant force F with the horizontal is given by:
`theta=tan^(-1)(F_y/F_x)`
Here, `F_x` = Total pressure force on the projected area of the curved surface on vertical plane, and
`F_y`= Weight of the liquid supported by the curved surface upto free surface of liquid which may be real or imaginary.
 Guest
Guest