Guest
Chapter:
1. Define total pressure force and centre of pressure. Derive an expressiom for m in various submerged case.
Total pressure is defined as the force exerted by a static fluid on a surface either plane or curved when the fluid comes in contact with the surfaces.
Centre of pressure is defined as the point of application of the total pressure on the surface.
There are generally four cases of submerged surface on which the total pressure force and the centre of pressure is to be determined:
Horizontal plane surface
Vertical plane surface
Inclined plane surface
Curved surfaceÂ
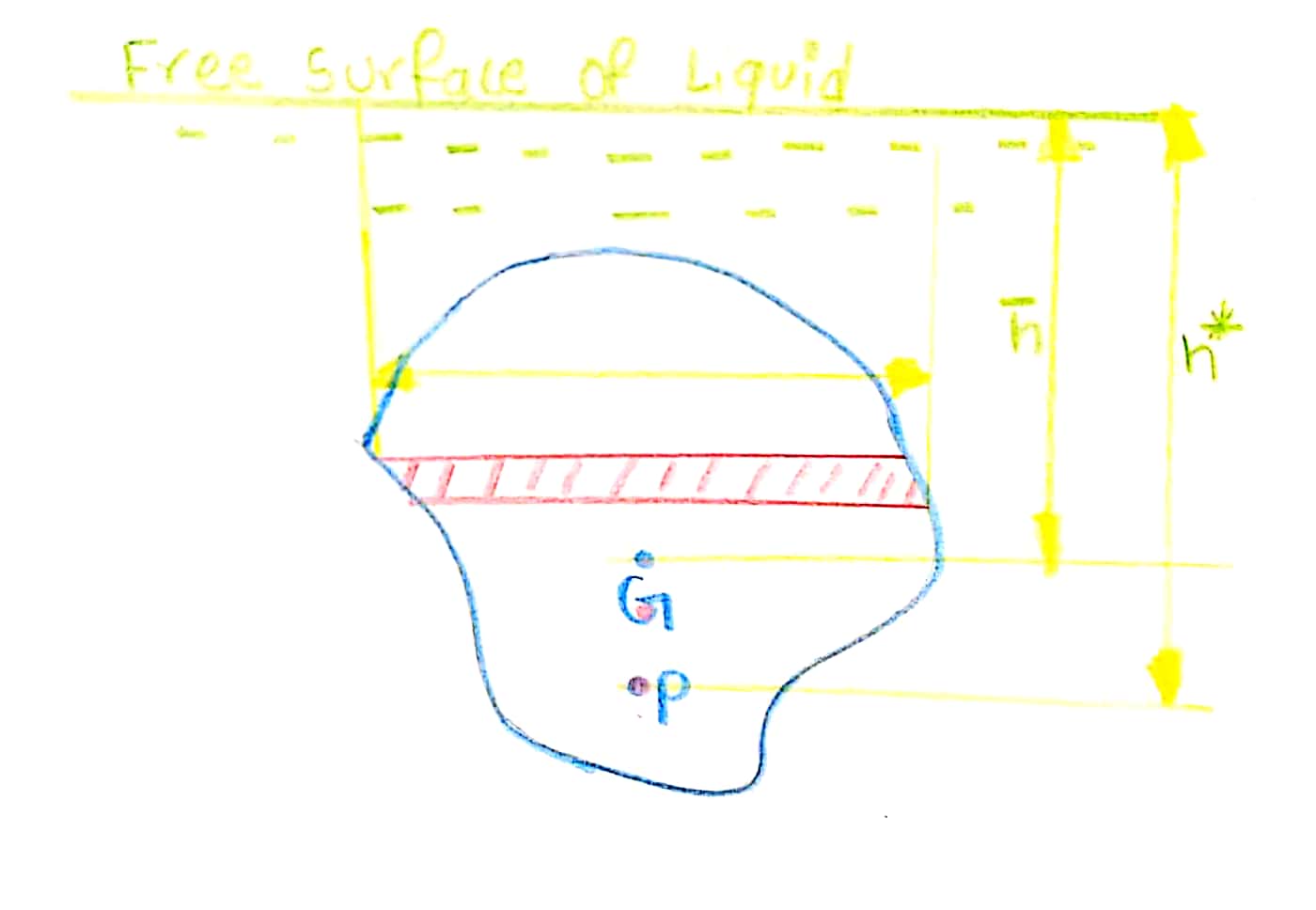
Vertical plane surface submerged in a liquid
Let us consider a plane vertical surface of arbitrary shape as shown in the figure.
Let,
A be the total area of the surface
`bar (h)` be the distance of C.G. of the area from the free surface of the liquid
G be the centre of gravity of the plane surface
P be the centre of pressure
`h^**` be the centre of pressure from free surface of the liquid
Let us consider a strip of thickness dh and width b at a depth h from the free surface of the liquid as shown in figure. Thus area of strip,`dA=b*dh`
Now, the pressure intensity on the strip is,`=rhogh`
The pressure force on the strip is,`dF=P*dA`
`=rhogh*bdh`
The total pressure force on the whole surface is,
`F=\int (rhogh*bdh)=rhog\int (bh*dh)`
But,`\int bh*dh=\inth*dA`
=moment of surface area about the free surface of liquid
=Area of surface ** distance of c.g. from free surface
`=A**bar (h)`
Thus,
`F=rhogA bar (h)`
Now the centre of pressure is calculated by using the principle of moments which states that the moment of the resulting force about an axis is equal to the sum of the moments of the components about the same axis.
The resulting force F is acting at P, at a distance `h^**` from the free surface of liquid as shown in figure. Hence moment of force F about free surface of liquid is `=F*h^**`
Similarly the moment of force dF acting on the strip about free surface of liquid is,
`=dF**h`
`=rhogh**bdh**h`
Sum of moments of all such forces about the free surface of liquid is,
`=\int (rhogh**bdh**h)`
`=rhog \int (h^2*bdh)`
`=rhog \int (h^2 dA)`
But,`\int h^2 dA=\int bh^2 dh=I_0`
=moment of inertia of the surface about the free surface of liquid.
Thus the sum of moments about free surface is,
`rhog*I_0`
or,`F*h^**=rhog*I_0`
`rhogA bar (h)*h^**=rhog*I_0`
`h^**=I_0/(A bar (h))`
Now,From the theorem of parallel axis,
`I_0=I_G+A(bar (h))^2`
Where, `I_G` is the moment of inertia about an axis passing through c.g. and parallel to the free surface of liquid.
Thus,
`h^**=(I_G+A(bar (h))^2)/(Abar (h))`
`h^**=I_G/(A bar (h))+bar (h)`
This is the expression for the centre of pressure which shows that
Centre of pressure lies below the centre of gravity
Centre of pressure is independent of the density of the liquid.
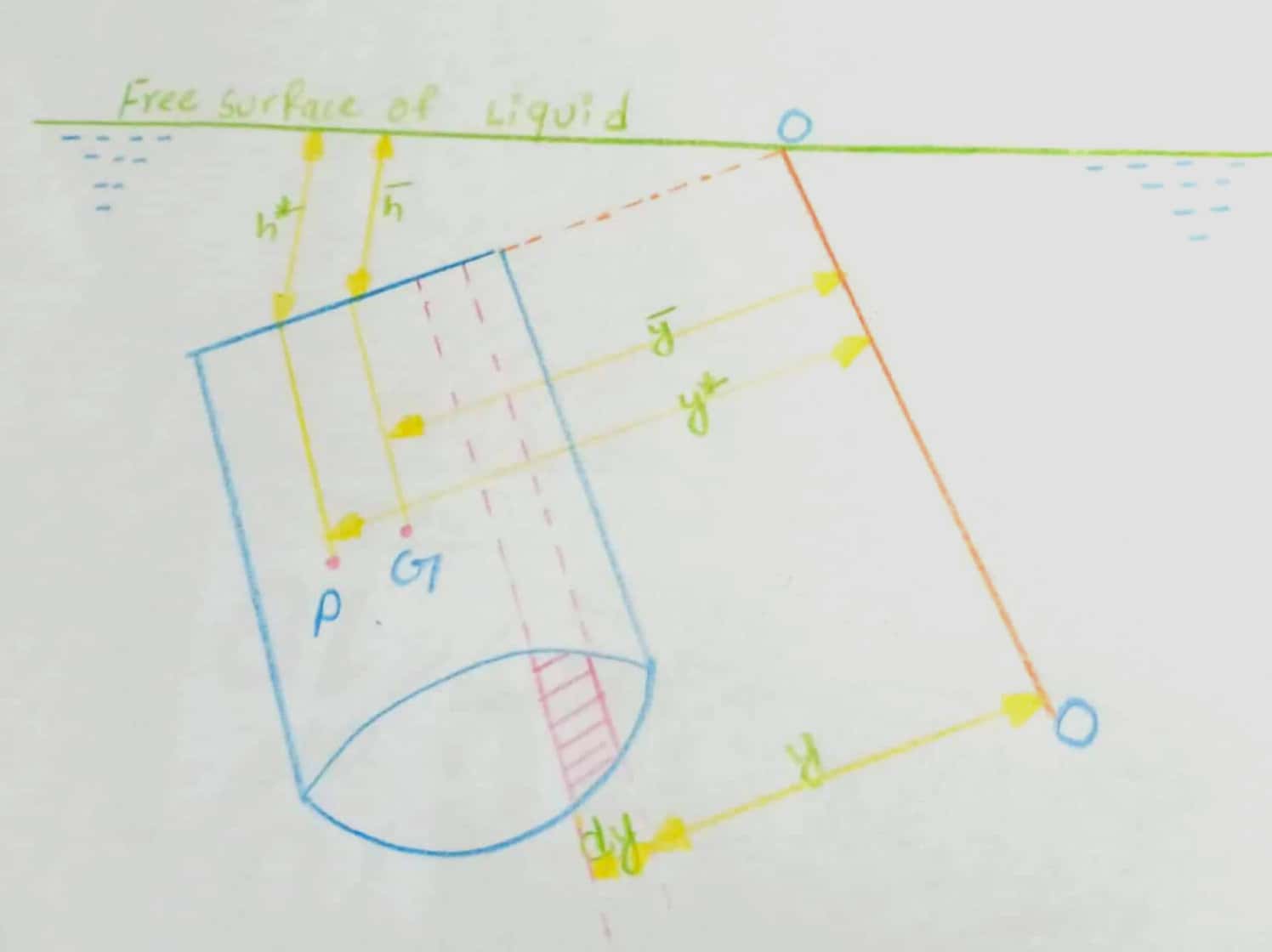
Inclined plane surface submerged in liquid:
Let us consider a plane surface of arbitrary shape immersed in a liquid in such a way that the plane makes an angle `theta` with the free surface of liquids as shown in figure.
Let,
A be the total area of the inclined surface
`bar (h)` be the distance of C.G. of the area from the free surface of the liquid
G be the centre of gravity of the plane surface
P be the centre of pressure
`h^**` be the centre of pressure from free surface of the liquid
Let the plane of the surface if produced meet the free liquid surface at O. Then O-O is the axis perpendicular to the pane of the paper.
Let,
`bar (y)` be the distance of the c.g. of the inclined surface from O-O
`y^**` be the centre of pressure from O-O.
Let us consider a strip of area dA.at a depth h from the free surface of the liquid and at a distance y from the axis O-O as shown in figure.Â
Now, the pressure intensity on the strip is,`=rhogh`
The pressure force on the strip is,`dF=P*dA`
`=rhogh*dA`
The total pressure force on the whole surface is,
`F=\int (rhogh*dA)`
From figure,
`h/y=bar (h)/(bar (y))=(h^**)/(y^**)=sintheta`
Thus,`h=ysintheta`
And,
`F=\int (rho*g*ysintheta*dA`
`=rhogsintheta \int(ydA)`
But,
`\int ydA=A*bar (y)`
`F=rhog sintheta*bar (y)*A`
`F=rhogA bar (h)`
Now the centre of pressure is calculated by using the principle of moments which states that the moment of the resulting force about an axis is equal to the sum of the moments of the components about the same axis.
The resulting force F is acting at P, at a distance `y^**` from the O-O axis as shown in figure. Hence moment of force F about free surface of liquid is `=F*y^**`
Similarly the moment of force dF acting on the strip about free surface of liquid is,
`=dF**h`
`=rhog*ysintheta**dA**h`
`=rhog sintheta*y^2 dA`
Sum of moments of all such forces about the O-O is,
`=\int (rhog sintheta*y^2 dA)`
`=rhog *sintheta \int (y^2*dA)`
But,
`\int y^2 dA=I_0`
=moment of inertia of the surface about the O-O.
Thus the sum of moments about O-O is,
`rhog*sintehta*I_0`
Thus,
or,`F*y^**=rhog*sintheta*I_0`
`rhogA bar (h)*h^**=rhog*I_0`
`y^**=(h^**)/(h sintheta)`
Now,From the theorem of parallel axis,
`I_0=I_G+A(bar (h))^2`
Where, `I_G` is the moment of inertia about an axis passing through c.g. and parallel to O-O.
Thus,
`(h^**)/(sintheta)=(rhog sintheta)/(rhogAbar (h))*(I_G+A*(bar (h))^2)`
But,
`bar (h)/bar (y)=sintheta`
`bar (y)=bar (h)/(sintheta)`
`h^**= (sin^2 theta)/(A bar (h))*(I_G+(A (bar (h))^2/(sin^2theta))`
`h^**=(I_G*sin^2 theta)/(A*bar (h))+bar (h)`
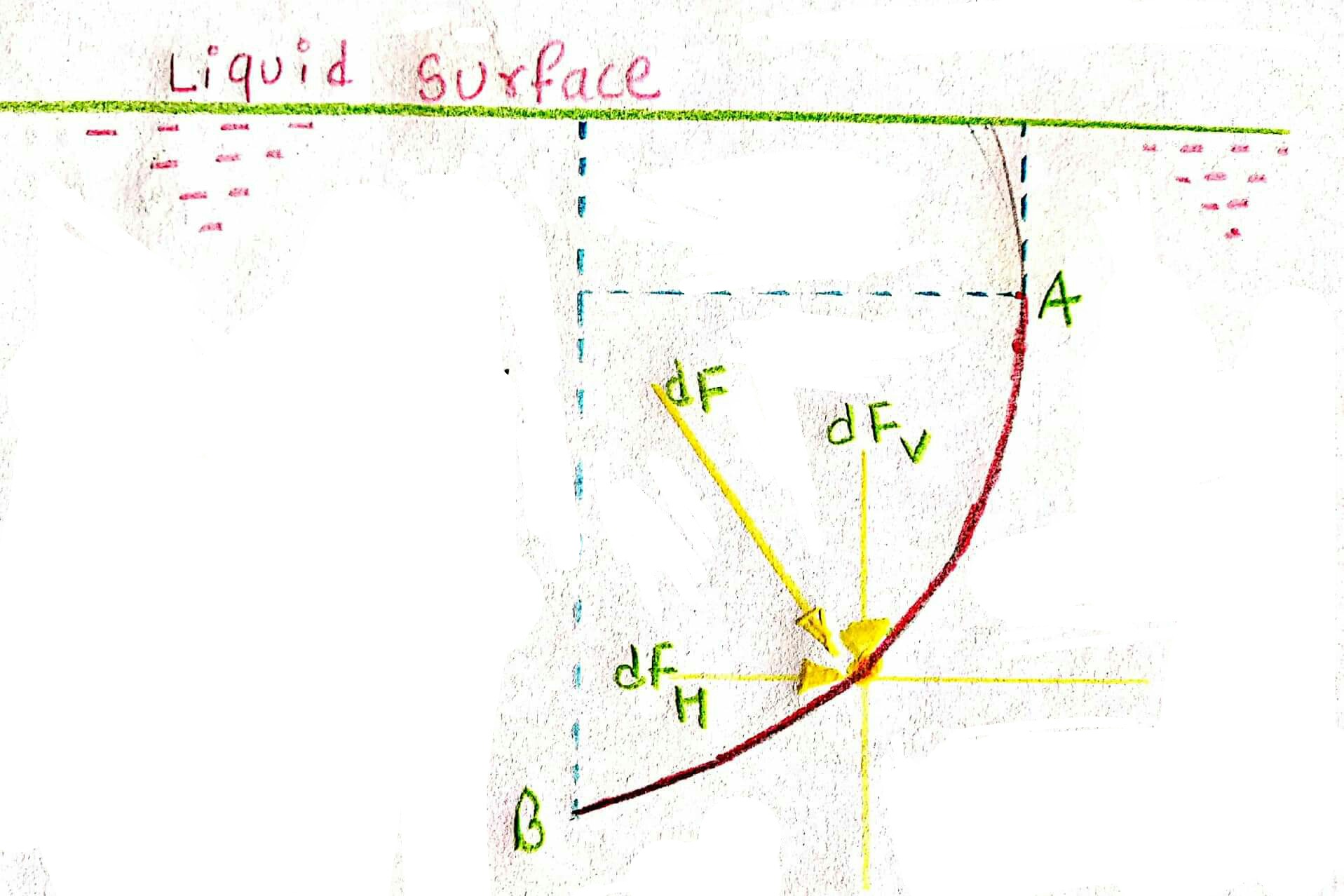
Curved submerged surfaceÂ
Consider a curved surface AB submerged in a static fluid as shown in figure. Let dA be the area of a small strip at a depth h from water surface.
Then pressure force on the area dA is,
`dF=rhogh*dA`
This force acts normal to the surface.
Hence total pressure force on curved surface should be,
`F=\int rhogh*dA`
But, in case of curved surface the direction of the total pressures on the elementary areas are not in the same direction, but varies from point to point. Thus the integration of above equation for curved surface is impossible.Â
The problem, however, can be solved by resolving the force F into horizontal and vertical components `F_H` and `F_V`.
Then total force on the curved surface is,
 `F=root ()((F_x)^2+(F_y)^2)`
The direction of the resultant force F with the horizontal is given by:Â
`theta=tan^(-1)(F_y/F_x)`
Here, `F_x` = Total pressure force on the projected area of the curved surface on vertical plane, and
`F_y`= Weight of the liquid supported by the curved surface upto free surface of liquid which may be real or imaginary.
2. A circular opening 3m in diameter in a vertical side of a tank is closed by a disc of 3m diameter which can rotate about a horizontal diameter. Calculate:
- force on disc
- torque required to maintain disc in equilibrium in vertical position ehen head of water above horizontal diameter is 4m
SOLUTION:
Given,
Diameter of circular opening, `d=3 m`
Thus area, `A=(pi*d^2)/4=7.068 m^2`
Depth of centre of gravity, `bar (h) =4 m`
Thus, the force on the disc is,
`F=rho*g*A*bar (h)`
`=1000**9.81**7.068**4`
`F=277368 N`
And the point of application of this force is,
`h^** =I_G/(A*bar (h))+bar (h)`
Where,
`I_G=`moment of inertia of the disc through it's centre of gravity.
For circular disc,
`I_G=(pi*d^4)/64`,
Thus,
`h^**=((pi*d^4)/64)/((pi*d^2)/4*bar (h))+bar (h)`
`=pi* d^2/(16**4)+4`
`h^**=4.14 m`
Thus the force acts at a distance of 4.14 m from the free surface of water. Now, taking moment of this force (i.e, torque) about a horizontal diameter, we get,
`=F*(h^** - bar (h))`
`=277368**(4.14-4)`
`=38831 Nm`
Hence, a torque of 38831 Nm must be applied on the disc in clockwise direction to maintain the disc in equilibrium position.
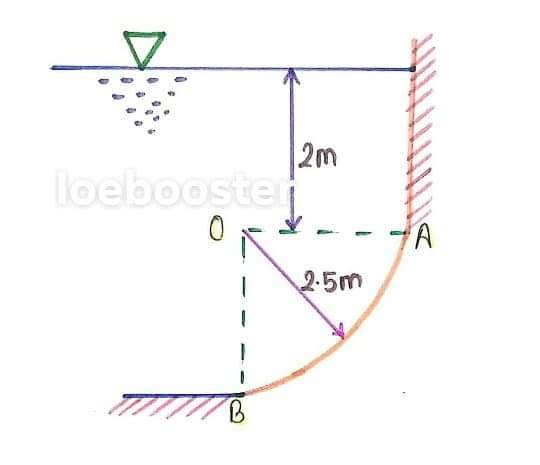
3. Find magnitude, direction and location of total pressure exerted by water on curved surface AB which is a quadrant of circular cylinder. Given that radius of surface is 2.5 m and cylinder is 3m long and water is 2 m above it.
SOLUTION:
Now,
The horizontal force is,
`F_x=rho*g*A*bar (h)`
`=9.81**(3**2.5)(2+2.5/2)`
`=239.11875 KN ->`
And it acts at a distance of,
`h^**=(I_G)/(A*bar (h))+bar (h)`
`=(3**2.5^3)/(12**(3**2.5)(2+2.5/2))+(2+2.5/2)`
`=3.41m` from the top.
Similarly,the vertical force is,
`F_y=rho*g**3 ((2.5**2)+(pi/4*2.5^2))`
`=291.614 KN`(downward)
And it acts at a c.g i.e,
`=(4r)/(3pi)=1.061m` towards right from O.
Thus,the resulting force,
`F=root ()(F_x^2+F_y^2)`
`=377.11 KN`
AND,
`theta=tan^-1 (F_y/F_x)=50.62^0`
4. A square aperture in vertical side of a tank has one diagonal vertical and is completely covered by plane plate hinged along one of upper sides of aperture. The diagonals of aperture are 2.4 m long and tank contains a liquid of specific gravity 1.2. The centre of aperture is 1.8 m below free surface. Calculate:
- thrust exerted on plate by liquid
- position of its centre of pressure
[ANNA UNIVERSITY ]
SOLUTION:
![A square aperture in the vertical side of a tank has one diagonal vertical and is completely covered by the plane plate hinged along one of the upper sides of the aperture. The diagonals of the aperture are 2.4 m long and the tank contains a liquid of specific gravity 1.2. The centre of aperture is 1.8 m below the free surface. Calculate:\r\n\r\n<ul>\r\n\r\n<li> the thrust exerted on the plate by the liquid</li>\r\n\r\n<li> the position of its centre of pressure</li>\r\n\r\n</ul>\r\n[ANNA UNIVERSITY ]](/img-uploads/1579773269.jpg)
Given,
Diagonal of aperture,PR=QS= 2.4 m
Area of square aperture, A= area of `triangle`PQR + area of `triangle`PSR
`A=2**1/2**2.4**2.4/2`
`A=2.88 m^2`
Now, the thrust exerted on the plate by the liquid is,
`F=rho*g*A*bar (h)`
`=1.2**1000**9.81**2.88**1.8`
`F=61026.05 N`
Again,
And the point of application of this force is,
`h^** =I_G/(A*bar (h))+bar (h)`
Where,
`I_G=`moment of inertia of aperture PQRS about the diagonal PR
=M.I of `triangle`PQR+M.I of `triangle`PSR about PR
`=(2.4**(1.2)^3)/12+(2.4**1.2^3)/12`
`=0.6912 m^4`
Thus,
`h^**=0.6912/(2.88**1.8)+1.8`
`h^**=1.933 m`
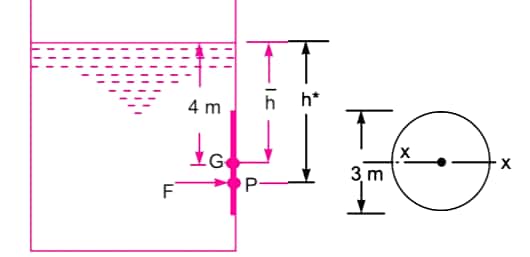
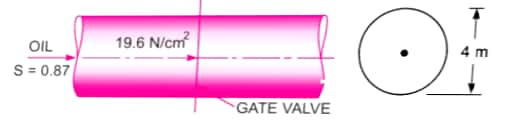
5. A pipeline which is 4m in diameter contains a gate valve. The pressure at centre of pipe is 19.6 N/`(cm)^2`. If pipe is filled with oil of specific gravity 0.87, Find force exerted by oil upon gate and position of center of gravity.
SOLUTION:
Given,
Diameter of pipe,`d=4 m`
Area of pipe,`A=(pi*d^2)/4=4pi m^2`
Pressure at the center of the pipe,`P=19.6**10^4`N/`m^2`
Now,
The pressure head at the centre is
`=p/(rho*g)=(19.6**10^4)/(870**9.81)=22.988 m`
Thus, the height of equivalent free surface of oil from the center of pipe = 22.988 m
Also, the depth of C.G of gate valve from free oil surface, `bar (h)=22.988 m`
Now,
Force on the gate is,
`F=rho*g*A*bar (h)=870**9.81**4pi*22.988`
`F=2465500 N`
Also,
the point of application of this force is,
`h^** =I_G/(A*bar (h))+bar (h)`
Where,
`I_G=`moment of inertia of pipe
For circular disc,
`I_G=(pi*d^4)/64`,
Thus, `h^**=((pi*d^4)/64)/((pi*d^2)/4*bar (h))+bar (h)`
`=0.043+22.988`
`h^**=23.031 m`Â
Thus the centre of pressure is acting at distance of 23.031 m from the imaginary free oil surface.
6. An opening in a dam is covered by use of a vertical sluice gate. The opening is 2 m wide and 1.2 m high. On upstream of gate liquid of specific gravity 1.45 lies upto a height of 1.5 m above top of gate, whereas on downstream side water is available upto a height touching top of gate. Find:
- The resultant force acting on gate and position of centre of pressure
- The force acting horizontally at top of gate which is capable of opening it.
Assume that gate is hinged at
bottom.
[Rajasthan University][A.M.I.E,May 1975]
SOLUTION:
Given,
![An opening in a dam is covered by the use of a vertical sluice gate. The opening is 2 m wide and 1.2 m high. On the upstream of the gate the liquid of specific gravity 1.45 lies upto a height of 1.5 m above the top of the gate, whereas on the downstream side the water is available upto a height touching the top of the gate. Find:<ul>\r\n\r\n<li> The resultant force acting on the gate and position of centre of pressure </li>\r\n\r\n<li>The force acting horizontally at the top of the gate which is capable of opening it.</li></ul>\r\n\r\n Assume that the gate is hinged at \r\n\r\nthe bottom.\r\n [Rajasthan University][A.M.I.E,May 1975]](/img-uploads/1579777006.jpg)
Width of the gate, `b = 2 m `
 Depth of the gate, `d = 1.2 m`
 Area, `A = b ** d = 2 ** 1.2 = 2.4 m^2`
 Specific gravity of liquid`S = 1.45`
Let,
`F_1` = Force exerted by the liquid of sp. gravity 1.45 on the gate, and
` F_2` = Force exerted by water on the gate.
`bar (h_1)` = the depth of C.G of the gate from free surface of liquid.i.e,
`bar (h_1)=1.5+1.2/2=2.1 m`
`bar (h_2)` = the depth of C.G of the gate from free surface of water.i.e,
`bar ( h_2)=1.2/2=0.6 m`
Now,the resultant force on the gate is
`F=F_1-F_2`
`=rho*g*A*bar (h_1)-rho*g*A*bar (h_2)`
`=1.45**1000**9.81**2.1-1000**9.81**0.6`
`F=57565 N`
We get,
`F_1=71691 N` and `F_2=14126 N`
Let the force `F_1` and `F_2` acts at a distance of `(h_1)^**` from the liquid surface and at a distance of `(h_2)^**` from the water surface respectively.
Now,
`(h_1)^** =I_G/(A*bar (h_1))+bar (h_1)`
Where,
`I_G=`moment of inertia
`I_G=(b*d^3)/12=(2**1.2^3)/12=0.288 m^4`
Thus,
`(h_1)^**=0.288/(2.4**2.1)+2.1=2.1571 m`
Now, the distance of point of application of `F_1` from the hinge is,
`=1.5+1.2-(h_1)^**`
`=1.5+1.2-2.1571`
`=0.5429 m`
Similarly,
`(h_2)^** =I_G/(A*bar (h_2))+bar (h_2)`
`(h_2)^**=0.288/(2.4**0.6)+0.6=0.8 m`
Now, the distance of point of application of `F_2` from the hinge is,
`=1.2-0.8`
`=0.4 m`
Thus, the resulting force `F` will be acting at a distance of,Â
`=(71691**0.5429-14126**0.4)/57565`
`=0.578 m` above the hinge.
Let `F ` is the force required on the top of the gate to open it. Now, taking moment about `F,F_1,F_2`, we get,
`F**1.2+F_2**0.4=F_1**0.5429`
Thus,`F=27725.5 N`
7. An inclined rectangular sluice gate AB 1.2 m by 5 m size shown in figure is installed to control discharge of water. The end A is hinged. Determine force normal to gate applied at B to open it. [A.M.I.E, Summer,1980]
SOLUTION:
Given,
![An inclined rectangular sluice gate AB 1.2 m by 5 m size shown in the figure is installed to control the discharge of water. The end A is hinged. Determine the force normal to the gate applied at B to open it. [A.M.I.E, Summer,1980]](/img-uploads/1579779790.jpg)
Size of the gate = 1.2 m ** 5 m
Area of the gate, `A=1.2**5=6 m^2`
Now,
The depth of C.G of the gate from free water surface is,
`bar (h)=5-(BG*cos45)`
`=5-(AB)/2cos45`
`=5-(1.2/2*1/root ()(2))`
`bar (h)=4.576 m`
Now, Total pressure force acting on the gate is,
`P=rho*g*A*bar (h)`
`=(1000**9.81**6**4.576)/1000`
`=269.3 KN`
Let, this force acts at a depth of `h^**`.
`h^**=(I_G sin^2theta)/(A*bar (h)+bar (h)`
`I_G=`moment of inertia
`I_G=(b*d^3)/12=(5**1.3^3)/12=0.72 m^4`
Thus,
`h^**=(0.72sin^2theta)/(6**4.576)+4.576`
`=4.589 m`
Now, taking moments about hinge A,we get,
`P**AC-F**1.2=0`
or,`269.3**AC=F**1.2`
From figure,
`AC=AB-BC`
`=AB-(OB-OC)`
`=AB-(5/(sin45)-(h^**)/(sin45))`
`=1.2-(5/(sin45)-4.589/(sin45))`
`=0.618`
Thus,
`F=(269.3**0.618)/1.2`
`F=138.69 KN`
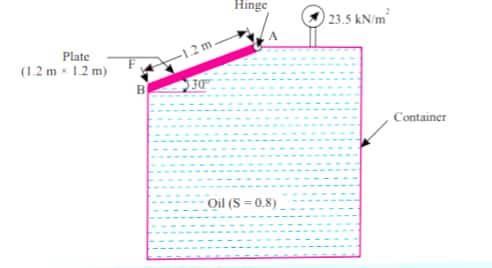
8. There is an opening in a container shown in figure below. Find force F and reaction at hinge.
SOLUTION:
Given,
Gauge pressure = 23.5 KN/`m^2`
`=23.5/(9.81**0.8)`
`=3 m` of oil.
Hence the free liquid surface may be considered to be 3 m further above the hinge as shown in figure. This free surface is known as imaginary free surface of oil.
Now, the distance of centroid of plate from the free oil surface is,
`bar (h)=3+(0.6 sin30)`
`=3.3 m`
Now, total pressure force on the plate AB is,
`P=rho*g*A*bar (h)`
`=0.8**1.2**1.2**9.81**3.3`
`=37.29 KN`
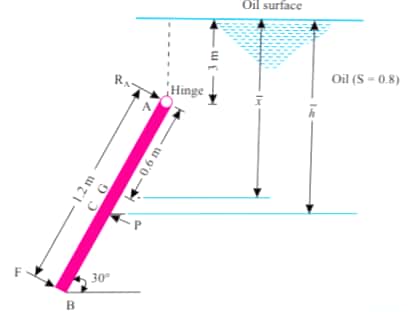
Let, this force acts at a depth of `h^**` from the imaginary oil surface.
`h^**=(I_G sin^2theta)/(A*bar (h))+bar (h)`
`I_G=`moment of inertia
`I_G=(b*d^3)/12`
Thus,
`h^**=((1.2**1.2^3)/12*sin^2(30))/(1.2**1.2**3.3)+3.3`
`=3.309m`
Now, taking moments about hinge A,we get,
`F**1.2-P*(AM)/(sin30)=0`
or,`F**1.2-37.29**(h^** -3)/(½)=0`
or,`F**1.2-37.29**2 (3.309-3)=0`
or,`F=19.2 KN`
Let, `R_A` be the reaction at the hinge.
Thus,
`R_A=P-F`
`=37.29-19.2`
`=18.09 KN`
9. A 3.6 m square gate provided in an oil tank is hinged at its top edge. This tank contains gasoline (s=0.7) upto a height of 1.8 m above top edge of plate. The space above oil is subjected to a negative pressure of 8250 N/`m^2`. Determine necessary vertical pull to be applied at lower edge to open gate. [GATE]
SOLUTION:
![A 3.6 m square gate provided in an oil tank is hinged at its top edge. This tank contains gasoline (s=0.7) upto a height of 1.8 m above the top edge of the plate. The space above the oil is subjected to a negative pressure of 8250 N/`m^2`. Determine the necessary vertical pull to be applied at the lower edge to open the gate.\r\n[GATE]](/img-uploads/1579781554.jpg)
Here, head of oil equivalent to negative pressure of 8250 N/`m^2` is,
`h=p/(rho*g)`
`=8250/(0.7**9810)`
`=1.2 m`
This negative pressure will reduce the oil head above the top edge of the gate from 1.8 m to 1.2 m i.e by 0.6 m.
This free surface is known as imaginary free surface.Â
Now, the distance of centroid of plate from the free surface is,
`bar (h)=0.6+(3.6/2*sin45)`
`bar (h)=1.873 m`
And,
Area,`A=3.6**3.6=12.96 m^2`.
The pressure force is,
`P=rho*g*A*bar (h)`
`=700**12.96**9.81**1.873`
`=166690N`
Let, this force acts at a depth of `h^**` from the imaginary surface.
`h^**=(I_G sin^2theta)/(A*bar (h)+bar (h)`
`I_G=`moment of inertia
`I_G=(b*d^3)/12`
Thus,
`h^**=((3.6**3.6^3)/12*sin^2(45))/(12.96**1.873)+1.873`
`h^**=2.16 m`
Now, taking moments about hinge A,we get,
`F**3.6sin45=P**(2.16-0.6)/(sin45)`
or, `F=144465 N`
This is the vertical force to be applied at the lower end of the gate to open the gate.
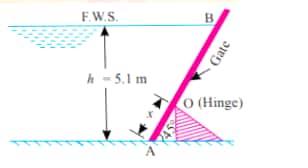
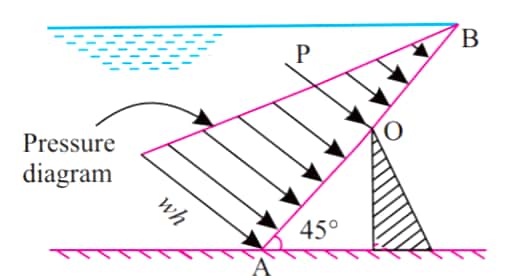
10. A gate supporting water takes form of an inclined shield which swings around a hinged axis O as shown in figure.Determine:
- The position x of hinge at which a water level of h = 5.1 m on left would cause gate to tip over hinge.
- The magnitude of hydrostatic free on gate just before it opens (tips about hinge) automatically
Neglect frictional effects.
SOLUTION:
The gate would tip about the hinge point O when the line of action of the resultant pressure force lies from O to B anywhere on the gate; the limiting condition being the situation when the resultant force passes through the hinged point O. Hence for the given condition point O becomes the centre of pressure.
The resultant also passes through the centroid of the pressure diagram, and the centroid lies at a distance `1/3** (AB) ` from the bottom point A.
Thus,
`x=â??*(AB)`
or, `AB=3*x`... (i)
Also,
`h=AB*sin45`
or,`h=3*x*sin45`
or,`h=2.4 m`
Now, the hydrostatic pressure force P is,
P = area of pressure diagram ** width of gate.
Assuming unit width of the gate,
`P=(1/2 *AB*wh*h)*1`
`=180.11 KN`
All Chapters
Dimensional Analysis, Similitude and Physical Modelling
Flow Past Through Submerged Body
Boundary Layer Theory
Properties of fluid
- properties of fluids
- complete IOE solution on fluid mechanics
- Detailed description chapterwise
- Unlimited Numericals problem solved with updation daily
- And much more
Hydrostatics
- Hydrostatics basic theory
- All important Numericals
- IOE,PU, MIT,A.M.I.E,Delhi university,EUPS,Engineering service exam solved problems
- Detailed explanation
Hydrostatics- Buoyancy and metacentric height
- detailed explanation of force of buoyancy, metacentric height,stability of floating body
- unlimited numericals solved with updation weekly
- including IOE , PU, KU, GATE, MIT, ANNA UNIVERSITY,UPSC EXAM SOLUTIONS
- And much more